Measurements and Their Analysis

​Population
- Consists of all possible observations that can be made on a particular item.
  - Thus can not be practically observed.
- Often a population has an infinite number of observations
- The mean and variance of a population are its true values

​Sample
- Subset of data collected from a population
- Can be collected in an economical fashion
- May or may not be representative of a population
- Size of same set influences its ability to predict true values of a population.
  - Larger samples generally have a higher probability of predicting true values.
​​
True Value
- A quantities theoretically correct or exact value.
  - True values are never known
  - Often we observe a calibration value with a more precise instrument using very precise techniques. These values are the used as true values with standard equipment.

Most Probable Value
- The most likely value for the true value as computed from a sample data set.
- For a simple set of repeated observations, this is the mean (average value).
​

Redundancies
- Also called degrees of freedom
- The number of observations in excess of the number necessary to solve for the unknowns.
 
How many redundancies are their if a distance is observed three times?

Methods of Analyzing Data

- Numerical methods
  - Range: The difference between the largest and smallest values in a set of data
    - That is, the largest discrepancy in a set of data
    - Also called dispersion.
  - Discrepancy: The difference between two elements in a set of data.
  - Measures of central tendency
    - Mean, median, mode
  - Measures of data variation
    - Variance, standard deviation 

- Graphical methods
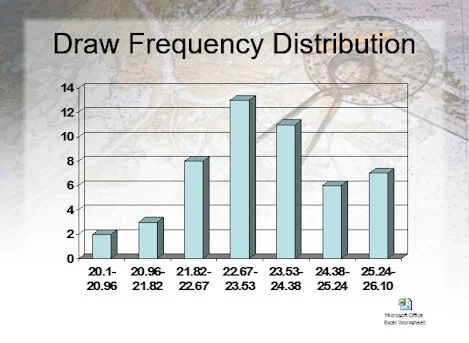
  - Frequency distribution: A bar graph based on a selected class width.
    - Also called a histogram
    - Class: A sub-region of data
    - Class width: range of a single class

- Median: The physical midpoint of a data set when the data is arranged in numerical order
  - If the data set has an odd number of elements, then it is the physical midpoint
  - If the data set has an even number of elements, then it is the average of the two points nearest to the physical midpoint.

Creating a Frequency Distribution
1. Select the number of classes
    - Typically between 5 and 10
2. Determine the class width
    - Class width = Range/(number of classes)
3. Create a class frequency table
    - Determine the number of elements in each class
4. Plot frequency of each class; i.e., create histogram.​
​

Things To Look For

- Notice the following when looking at a histogram
  - Symmetry about central values
  - Range of data set
  - Frequency of occurrence of measured values
  - Steepness of histogram
    - Measure of precision
      - The steeper the slopes of the sides are the more precise the data.

- How to Lie with a bar graph
  - ​Note lowest value in histogram
  - ​When comparing two data sets, they must use the same class width